Abstract
Background: Sensitivity and specificity are characteristics of a diagnostic test and are not expected to change as the prevalence of the target condition changes. We sought to evaluate the association between prevalence and changes in sensitivity and specificity.
Methods: We retrieved data from meta-analyses of diagnostic test accuracy published in the Cochrane Database of Systematic Reviews (2003–2020). We used mixed-effects random-intercept linear regression models to evaluate the association between prevalence and logit-transformed sensitivity and specificity. The model evaluated all meta-analyses as nested within each systematic review.
Results: We analyzed 6909 diagnostic test accuracy studies from 552 meta-analyses that were included in 92 systematic reviews. For sensitivity, compared with the lowest quartile of prevalence, the second, third and fourth quartiles were associated with significantly higher odds of identifying a true positive case (odds ratio [OR] 1.17, 95% confidence interval [CI] 1.09–1.26; OR 1.32, 95% CI 1.23–1.41; OR 1.47, 95% CI 1.37–1.58; respectively). For specificity, compared with the lowest quartile of prevalence, the second, third and fourth quartiles were associated with significantly lower odds of identifying a true negative case (OR 0.74, 95% CI 0.69–0.80; OR 0.65, 95% CI 0.60–0.70; OR 0.47, 95% CI 0.44–0.51; respectively). Pooled regression coefficients from bivariate models conducted within each meta-analysis showed that prevalence was positively associated with sensitivity and negatively associated with specificity. Findings were consistent across subgroups.
Interpretation: In this large sample of diagnostic studies, higher prevalence was associated with higher estimated sensitivity and lower estimated specificity. Clinicians should consider the implications of disease prevalence and spectrum when interpreting the results from studies of diagnostic test accuracy.
Clinicians practising evidence-based medicine are familiar with the concepts of sensitivity and specificity, defined as the probability of a positive test given that the person has the target condition, and the probability of a negative test given that the person does not have the condition, respectively.1 In practice, sensitivity and specificity are often treated as being independent from disease prevalence, defined as pre-test probability of disease or probability of the target condition in the study sample. This is often contrasted with positive and negative predictive values or post-test probabilities, which are highly dependent on prevalence and pretest probability. Therefore, sensitivity and specificity are considered to be characteristics of the test as intrinsic accuracy measures, and independent from the characteristics of the population. The rationale for this assumption relates to the mathematical calculation of these measures from a classic 2 × 2 diagnostic table.
However, sensitivity and specificity have been found to change as disease prevalence changes. Leeflang and colleagues2 provided 4 examples of individual diagnostic studies in which sensitivity and specificity changed as the prevalence changed, and Li and Fine3 showed the same in 2 meta-analyses. In a separate study, Leeflang and colleagues4 used data from 23 meta-analyses and evaluated the effects of prevalence on sensitivity and specificity using a bivariate random-effects model for each meta-analysis, with prevalence as a covariate.5,6 The results suggested that specificity tended to be lower with a higher prevalence, whereas sensitivity changes did not follow a specific pattern.4
Overall, however, the number of studies that have evaluated the association between prevalence and sensitivity and specificity is small, although the issue is very important. Some of the reported changes in sensitivity and specificity reached 40 percentage points,4 which can entirely change the impact of the test in management of patients and can lead to more false positives and negatives, under- and overdiagnosis, and possible harm to patients. Therefore, we sought to evaluate the relationship between prevalence and sensitivity and specificity in a large sample of studies of diagnostic test accuracy.
Methods
We conducted a meta-epidemiological study using diagnostic meta-analyses published by the Cochrane Collaboration. This study follows the reporting guideline for meta-epidemiological methodology research.7
Data source and study selection
We searched all reviews flagged as diagnostic test accuracy reviews in the Cochrane Database of Systematic Reviews published between January 2003 and January 2020. To be included, eligible meta-analyses had to report a classic 2 × 2 diagnostic table (i.e., true positive, false positive, false negative and true negative results) and include at least 4 studies. We did not restrict by patient population, type of diagnostic test, study location or condition studied. We excluded diagnostic studies that had a case–control design, in which disease prevalence is not reliably estimated and may not reflect the true population disease prevalence, severity or spectrum.
Data extraction
We used the RCurl package in R to download data from the RM5 files of the systematic reviews from the Cochrane Database of Systematic Reviews. We converted these to comma-separated values files for analyses. In addition to 2 × 2 diagnostic tables, we extracted author names and publication time of the original studies of diagnostic test accuracy, as well as the systematic reviews. Pairs of reviewers independently and manually extracted the overall risk of bias across original studies, test type, study setting and target condition. We used the QUADAS-2 tool in evaluating risk of bias.8 Reviewers also extracted whether the systematic reviews explicitly discussed spectrum bias or spectrum effect as a possible modifier of diagnostic accuracy, and if the reviews conducted subgroup analyses based on prevalence.
Outcome
Our outcome of interest was the association between prevalence and sensitivity and specificity.
Statistical analysis
In the main analysis, we fitted 2 separate models to evaluate the association between prevalence and logit-transformed sensitivity or logit-transformed specificity. These models were 3-level, mixed-effects, random-intercept linear regression models. Fixed effects included disease prevalence, categorized as quartiles based on the distribution within a meta-analysis (≤ 25th percentile as reference, 26th–50th percentile, 51st–75th percentile and > 75th percentile) or arbitrary prevalence cut-offs (< 25%, 26%–50%, 51%–75%, > 75%), adjusting for the target condition category (collapsed into 5 categories based on the discipline or specialty, namely internal medicine, surgery, oncology, obstetrics and gynecology, and neurology or psychiatry), type of diagnostic test (pathology and cytology, blood test, imaging, physical examination or symptomatology, urine or cerebrospinal fluid test and a category of multiple test types), study setting (inpatient, outpatient and mixed) and risk of bias (low, high and unclear). We included random effects for each meta-analysis and, then, nested within each systematic review. In a sensitivity analysis, we added the slope of prevalence as a random effect in the 3-level mixed effects model (Appendix 1, available at www.cmaj.ca/lookup/doi/10.1503/cmaj.221802/tab-related-content).
In a secondary analysis, we applied a bivariate mixed-effects regression model to jointly estimate sensitivity and specificity for each individual meta-analysis,5 and added the estimated prevalence (proportion of people with the target condition in each study) as a continuous covariate to the model. To estimate the direction and strength of the association between prevalence and logit-transformed sensitivity and specificity, we pooled regression coefficients of prevalence as estimated from each meta-analysis using the restricted maximum likelihood random-effects method. We conducted subgroup analyses based on category of target condition, type of diagnostic test, study setting and risk of bias.
We graphed trends of logit-transformed sensitivity and specificity against prevalence using a locally weighted scatterplot smoothing plot. We considered a 2-tailed p value of less than 0.05 statistically significant. We conducted all statistical analyses using Stata/SE, version 17.0 (StataCorp LLC). Analysis codes are listed in Appendix 1.
Ethics approval
Ethics approval was not needed for this analysis.
Results
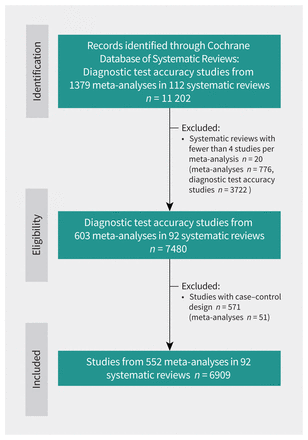
We retrieved data from 112 systematic reviews of diagnostic test accuracy. After exclusions, we analyzed 6909 studies of diagnostic accuracy (i.e., 6909 2 × 2 tables) from 552 meta-analyses that were included in 92 systematic reviews (Figure 1). The individual diagnostic accuracy studies were published between 1961 and 2019, with a median sample size of 157 (interquartile range [IQR] 74–404) patients. The median number of original diagnostic accuracy studies within a meta-analysis was 17 (IQR 5–34) studies. Across the 552 meta-analyses, the median prevalence ranged from 0.07% to 94.90% (IQR 11.65%–41.15%). Only 14 (15.2%) of the 92 systematic reviews explicitly discussed spectrum bias or spectrum effect as a possible modifier of diagnostic accuracy, and only 7 (7.6%) conducted subgroup analyses based on prevalence.
Study flow chart. A systematic review could include several meta-analyses. Individual diagnostic test accuracy studies refer to original studies included in each meta-analysis.
The association of prevalence with sensitivity and specificity
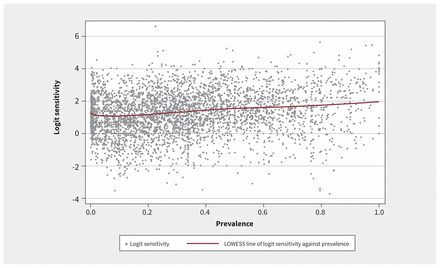
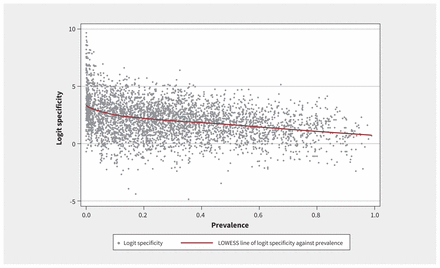
Figure 2 shows a positive association between sensitivity and prevalence, and Figure 3 shows a negative association between specificity and prevalence. In the main analysis, we fitted a mixed-effects model with random effects for each meta-analysis nested within each systematic review. Table 1 shows the results stratified by prevalence quartiles and arbitrary prevalence cutoffs (25%, 50%, 75% and 100%). For sensitivity, compared with the lowest quartile of prevalence, the second, third and fourth quartiles were associated with significantly higher odds of identifying a true positive case (odds ratio [OR] 1.17, 95% confidence interval [CI] 1.09–1.26; OR 1.32, 95% CI 1.23–1.41; OR 1.47, 95% CI 1.37–1.58; respectively). For specificity, compared with the lowest quartile of prevalence, the second, third and fourth quartiles were associated with significantly lower odds of identifying a true negative case (OR 0.74, 95% CI 0.69–0.80; OR 0.65, 95% CI 0.60–0.70; OR 0.47, 95% CI 0.44–0.51; respectively). The sensitivity analyses in which prevalence was modelled as a random intercept and random slope showed similar findings (Appendix 1).
Locally weighted scatterplot smoothing (LOWESS) plot of logit-transformed sensitivity against prevalence, showing a positive association between prevalence and sensitivity.
Locally weighted scatterplot smoothing (LOWESS) plot of logit-transformed specificity against prevalence, showing a negative association between prevalence and specificity.
Mixed-effects model incorporating all meta-analyses*
In the secondary analysis (Table 2), the pooled regression coefficients of prevalence from bivariate regression models showed the direction and strength of the association between prevalence and sensitivity and specificity. In this analysis, data from 379 individual studies failed to converge. Thus, the analysis included 6530 diagnostic test accuracy studies. Among the 6530 studies, the target condition categories included internal medicine (n = 2755, 42.2%), oncology (n = 1693, 25.9%), obstetrics and gynecology (n = 937, 14.3%), neurology or psychiatry (n = 578, 8.9%) and surgery (n = 567, 8.7%). The most common diagnostic test types were pathology and cytology (n = 1369, 21.0%), blood tests (n = 1310, 20.1%), imaging (n = 1334, 20.4%) and physical examination or symptomatology (n = 1174, 18.0%). The tests were conducted in outpatient settings (n = 1662, 25.5%), hospital settings (n = 929, 14.2%) and settings that were mixed or unclear (n = 3939, 60.3%). The risk of bias of the 6530 original studies was high in 1818 (27.8%) studies, low in 2841 (43.5%) studies and unclear in 1871 (28.7%) studies. The findings suggest a positive association with logit-transformed sensitivity (mean 0.92, standard error 0.10) and a negative association with logit-transformed specificity (mean −7.43, standard error 2.10). Findings were consistent across subgroups.
Pooled regression coefficients of prevalence from bivariate regression models
Interpretation
We performed a meta-epidemiological analysis of 6909 studies of diagnostic tests and found that sensitivity is positively associated with prevalence, whereas specificity is negatively associated with prevalence. The direction of this change was also found in the secondary analyses in which a bivariate model incorporated prevalence as a covariate within each meta-analysis.
Our results are consistent with other studies that have attempted to evaluate whether there is an association between prevalence and sensitivity and specificity.2–4,9 In terms of the direction of the association and its pattern, other studies suggested that specificity tended to be negatively associated with prevalence, as we observed, whereas sensitivity changes did not follow a specific pattern.2–4 However, these studies were far smaller and may have been underpowered.
Although the definitions of sensitivity and specificity do not depend on prevalence, our results support the existence of such an association. Spectrum bias, also called spectrum effect, could partially explain this association.2,10,11 A test may perform better when used to evaluate patients with more severe disease than it would in patients whose disease is less obvious or less advanced. Hence, if investigators choose clinically inappropriate populations when studying a diagnostic test, they can introduce spectrum bias, which may seriously affect the results to show that the test performs better than it actually does. Disease status is not truly binary; rather, a spectrum of continuous traits defines disease severity (e.g., serum glucose and a diagnosis of diabetes).9 Patients with test values close to the test cut-off are more likely to be misclassified. This misclassification is correlated with population characteristics and prevalence.2,10,11 Therefore, prevalence may be a surrogate for disease severity, and thus affects sensitivity and specificity. Brenner and Gefeller9 evaluated the effect of a hypothetical continuous trait that categorizes people into diseased and not diseased, and found that the dependence of sensitivity on prevalence may be of similar magnitude to that of the positive predictive value. They expected that, as prevalence increases, sensitivity would increase and specificity would decrease, similar to our findings.9
The design of diagnostic studies and enrolment procedures could lead to increased spectrum effect. For example, test accuracy studies that enroll patients from subspecialty clinics may include higher prevalence and sicker patients than when the test is conducted in a primary care clinic because of referral bias.2 The association between accuracy and prevalence may have other explanations. For example, Leeflang2 suggests that an inadequate or imperfect reference standard will underestimate accuracy, but this effect may decline at a higher prevalance. The observed association between test accuracy and prevalence may also be related to the fact that it was evaluated within a meta-analysis and therefore reflects sample sensitivity and specificity, whereas the population sensitivity and specificity remain theoretically independent.3
For evidence-based practitioners, the current findings suggest that when they apply evidence about diagnostic accuracy of a test, they should compare the prevalence of disease in their context with that in available studies. A very different prevalence may indicate a different disease spectrum and uncertainty about the sensitivity and specificity. This uncertainty also affects the likelihood ratios, which are derived from sensitivity and specificity and may have a stronger association with prevalence.9
For researchers conducting original studies on diagnostic accuracy, special attention should be paid to the spectrum of the disease in their sample so that it is consistent with the spectrum of disease among people who will receive the test in practice. In addition, when the spectrum or prevalence of disease is highly variable, researchers should plan stratified analyses by disease severity and spectrum.
For researchers conducting systematic reviews of diagnostic test studies, our results suggest the need to consider the effect of prevalence on diagnostic accuracy measures. They may consider conducting subgroup analyses by prevalence (e.g., low, medium, high), although these exploratory analyses can be affected by chance findings and errors related to the arbitrary categorizing of prevalence into discrete categories. Another approach that may avoid some of these limitations is to jointly model disease prevalence with diagnostic test sensitivity and specificity, such as by using trivariate generalized linear mixed models.12–14 Such models can directly estimate the correlations between diagnostic accuracy measures with prevalence on a logit-transformed scale, but require a large number of studies (> 10) to achieve model convergence.
Limitations
Although the large number of studies of diagnostic test accuracy included in this analysis represents a strength, it also made granular evaluation at a study level infeasible for some factors. We were able to address only risk of bias, target condition, study setting and diagnostic test type. Other causes of variability include the stringency or misclassification of the gold-standard test or the threshold used to categorize study participants as positive for the target condition; these may have contributed to the observed association with prevalence. Spectrum bias or effect was not explored by most of the systematic reviews evaluated in this study; hence, we did not have sufficient information to further explore this issue. We also acknowledge the heterogeneity across the studies, which we addressed by clustering the regression analysis within each meta-analysis, given that the authors had decided that the studies were sufficiently similar to include in the same meta-analysis. Random measurement error and variability in prevalence may lead to regression dilution bias, although such bias would likely drive the estimated association toward the null.15 Despite our effort in excluding duplicate and overlapping studies or participants, this possibility still exists, which is a limitation of meta-epidemiological research in which the study is the unit of analysis.
Conclusion
We found that the estimated sensitivity and specificity of diagnostic tests are associated with the prevalence of the target condition. Prevalence could be a surrogate of disease spectrum and should be considered when interpreting the results of studies that evaluate diagnostic test accuracy.
Footnotes
Competing interests: Haitao Chu is employed by Pfizer and owns stock in the company. No other competing interests were declared.
This article has been peer reviewed.
Contributors: M. Hassan Murad and Zhen Wang contributed to the conception and design of the work. Bashar Hasan, Reem Alsibai and Alzhraa Abbas contributed to data acquisition; Lifeng Lin, Haitao Chu, Bashar Hasan, Reem Alsibai, Alzhraa Abbas and Zhen Wang contributed to data analysis. All of the authors contributed to interpretation of data. M. Hassan Murad and Zhen Wang drafted the manuscript. All of the authors revised it critically for important intellectual content, gave final approval of the version to be published and agreed to be accountable for all aspects of the work.
Funding: Lifeng Lin is supported by the United States National Institute of Mental Health (R03 MH128727) and the US National Library of Medicine (R01 LM012982).
Data sharing: All data are publicly available. The RCurl package of R can be used to download data from the .rm5 files of the systematic reviews from the Cochrane Database of Systematic Reviews.
- Accepted June 1, 2023.
This is an Open Access article distributed in accordance with the terms of the Creative Commons Attribution (CC BY-NC-ND 4.0) licence, which permits use, distribution and reproduction in any medium, provided that the original publication is properly cited, the use is noncommercial (i.e., research or educational use), and no modifications or adaptations are made. See: https://creativecommons.org/licenses/by-nc-nd/4.0/